Determination of ∆H(combustion)
by bomb calorimetry.
by bomb calorimetry.
Introduction
Calorimeter Calibration
Unknown analysis

Bomb calorimetry is a technique that allows you to directly measure the heat of combustion of a sample. Bomb refers to the heavy metal container in which the sample is combusted. This container is pressurized to many atmospheres of pure oxygen to promote rapid and full combustion of the sample to products such as N2, CO2 and H2O.
The heat released by the combustion, can produce temperatures as high as 1500°C inside the bomb. This heat is captured by the thermal mass of the bomb and an enclosing water bath of known mass. Because the bomb and water bath are thermally isolated from the outside world, they are called an adiabatic system.
The heat released by the combustion, can produce temperatures as high as 1500°C inside the bomb. This heat is captured by the thermal mass of the bomb and an enclosing water bath of known mass. Because the bomb and water bath are thermally isolated from the outside world, they are called an adiabatic system.
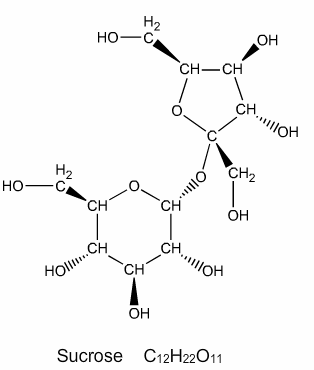
In this experiment we will be determining the heat of combustion of an unknown compound. This compound is similar to sucrose; common table sugar. We will use sucrose for illustrative purposes during this introduction.
The empirical formula of sucrose is C12H22O11 and its structure can be seen to the left. The molar mass of sucrose is calculated to be 342.3 g/mol.
The combustion reaction produces CO2 and H2O.
C12H22O11(s) + 12 O2(g) → 12 CO2(g) + 11 H2O(I)
The empirical formula of sucrose is C12H22O11 and its structure can be seen to the left. The molar mass of sucrose is calculated to be 342.3 g/mol.
The combustion reaction produces CO2 and H2O.
C12H22O11(s) + 12 O2(g) → 12 CO2(g) + 11 H2O(I)
During the experiment we measure the change in temperature inside our adiabatic system (consisting of the water bath, the bomb and its contents).
Thermodynamics tell us
∆U = q + w + E(kinetic) + E(potential)
U is the internal energy of our adiabatic system. Any change in internal energy will result in a loss or gain of heat (q), work (w) reflected by a change in volume, kinetic energy as motion, or potential energy as an elevation.
Since our system is adiabatic (thermally isolated), q = 0. Also, since the volume is constant, w = 0. Changes in kinetic and potential energy are also zero as the system is immobile and its position unchanged.
Since any generated heat is contained in the system, and no work was done, the change in internal energy ∆U = 0
Thermodynamics tell us
∆U = q + w + E(kinetic) + E(potential)
U is the internal energy of our adiabatic system. Any change in internal energy will result in a loss or gain of heat (q), work (w) reflected by a change in volume, kinetic energy as motion, or potential energy as an elevation.
Since our system is adiabatic (thermally isolated), q = 0. Also, since the volume is constant, w = 0. Changes in kinetic and potential energy are also zero as the system is immobile and its position unchanged.
Since any generated heat is contained in the system, and no work was done, the change in internal energy ∆U = 0
So ∆U = 0 tells us that the calorimeter plus reactants at room temperature has the same internal energy as the calorimeter plus products at an elevated temperature. During the experiment, the products are formed and the system is heated simultaneously. U is a state function which means that its value depends on the system's current condition and not on how it got there. Therefore we can consider combustion and heating as two separate steps which together give the same overall result.
∆U(overall) = ∆U(combustion) + ∆U(heating)
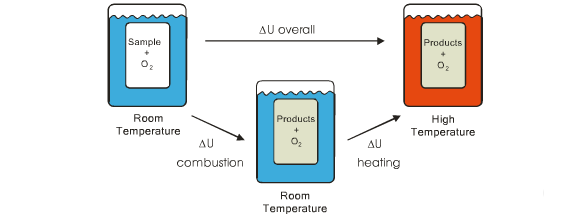

We've seen that the overall change in the internal energy of our system is zero. Combining this with the knowledge that we can treat the combustion and heating separately yields ...
∆U(overall) = ∆U(combustion) + ∆U(heating) = 0 or by simple rearrangement that
∆U(combustion) = -∆U(heating)

∆U(overall) = ∆U(combustion) + ∆U(heating) = 0 or by simple rearrangement that
∆U(combustion) = -∆U(heating)

∆U(heating) can be calculated as the heat capacity of the system times the change in temperature.
∆U(heating) = Cv(T2 - T1)
So finally we arrive at ...
∆U(combustion) = -∆U(heating) = -Cv(T2 - T1)
The enthalpy of combustion, ∆H(combustion), is related to
∆U(combustion) by ...
∆H(combustion) = ∆U(combustion) + RT(combustion)∆n(gas)
where R is the gas constant, T(combustion) is the temperature of the system and ∆n(gas) is the change in the number of moles of gas due to the reaction.
∆U(heating) = Cv(T2 - T1)
So finally we arrive at ...
∆U(combustion) = -∆U(heating) = -Cv(T2 - T1)
The enthalpy of combustion, ∆H(combustion), is related to
∆U(combustion) by ...
∆H(combustion) = ∆U(combustion) + RT(combustion)∆n(gas)
where R is the gas constant, T(combustion) is the temperature of the system and ∆n(gas) is the change in the number of moles of gas due to the reaction.
Using the fact that ∆U(combustion) = -∆U(heating) gives us our final equation
∆H(combustion) = -Cv(T2 - T1) + RT(combustion)∆n(gas)
T1 and T2 will be measured during the experiment. ∆n(gas) is given by the stoichiometry of the reaction. T(combustion) will be set to 298K, and R is the gas constant. Only Cv is unknown.
Our first task will therefore be to determine Cv by burning a compound with a known ∆H(combustion). A good compound to use is benzoic acid which has a
∆H(combustion) = -3227 kJ/mol and a molar mass of 122.12 g/mol.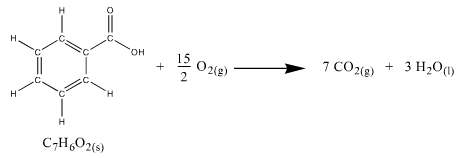
∆H(combustion) = -Cv(T2 - T1) + RT(combustion)∆n(gas)
T1 and T2 will be measured during the experiment. ∆n(gas) is given by the stoichiometry of the reaction. T(combustion) will be set to 298K, and R is the gas constant. Only Cv is unknown.
Our first task will therefore be to determine Cv by burning a compound with a known ∆H(combustion). A good compound to use is benzoic acid which has a
∆H(combustion) = -3227 kJ/mol and a molar mass of 122.12 g/mol.

Thus the heat of combustion per gram of benzoic acid is
( -3227 kJ/mol / 122.12 g/mol ) = -26.42 kJ/g.
Note that, as expected, the heat of combustion has a negative sign. Cv will be a positive quantity.

( -3227 kJ/mol / 122.12 g/mol ) = -26.42 kJ/g.
Note that, as expected, the heat of combustion has a negative sign. Cv will be a positive quantity.


In the next section of this experiment you will calibrate a bomb calorimeter to familiarize yourself with the equipment.
In the third and final section you will use an other bomb calorimeter that has been calibrated for you to determine the heat of combustion of an unknown sample.
In the third and final section you will use an other bomb calorimeter that has been calibrated for you to determine the heat of combustion of an unknown sample.

Bomb calorimetry is a technique that allows you to directly measure the heat of combustion of a sample. The heat released by combustion is captured by the thermal mass of the bomb and the enclosing water bath.
Because the bomb and water bath are thermally isolated from the outside world, any change in their temperature is a result of the heat of combustion.
If we know the heat capacity of the bomb and water bath we can relate the temperature change to the amount of heat released by burning the sample.
Because the bomb and water bath are thermally isolated from the outside world, any change in their temperature is a result of the heat of combustion.
If we know the heat capacity of the bomb and water bath we can relate the temperature change to the amount of heat released by burning the sample.
The easiest way to determine the heat capacity of our bomb calorimeter is to burn a sample with a well known ∆H(combustion).
A good compound to use is benzoic acid which has a ∆H(combustion) = -3227 kJ/mol and a molar mass of 122.12 g/mol. This corresponds to a heat of combustion per gram of benzoic acid of -26.42 kJ/g.
Then we can calculate the heat capacity of the calorimeter as
Cv = - ( ∆H(combustion) - RT(combustion)∆n(gas) ) / (T2 - T1)
A good compound to use is benzoic acid which has a ∆H(combustion) = -3227 kJ/mol and a molar mass of 122.12 g/mol. This corresponds to a heat of combustion per gram of benzoic acid of -26.42 kJ/g.
Then we can calculate the heat capacity of the calorimeter as
Cv = - ( ∆H(combustion) - RT(combustion)∆n(gas) ) / (T2 - T1)

The bomb calorimeter that you will be calibrating has a serial number.
6493
Be sure to record this number as it will allow the calculated Cv to be associated with the correct device.
6493
Be sure to record this number as it will allow the calculated Cv to be associated with the correct device.
A pellet press has been used to form approximately 1g of benzoic acid into a pellet. To weigh the pellet accurately we will first weigh an empty beaker. Next press the 'Weigh Benzoic Acid' button. This will place a pellet of benzoic acid into the beaker.
The increase in weight will correspond to the weight of the pellet.
Once you've recorded these two weights, press the 'Use O2 Bomb' button.
The increase in weight will correspond to the weight of the pellet.
Once you've recorded these two weights, press the 'Use O2 Bomb' button.
This is the O2 bomb head. It contains a small metal cup which holds the sample. A fuse that ignites the sample is attached between two posts. Electrical connections pass through the head so that the fuse can be remotely triggered. Also, connections are provided to pressurize the bomb with oxygen and to vent it afterwards.
Press 'Load Sample' to transfer the benzoic acid pellet from the beaker into the sample holder. Be careful not to chip the pellet when doing such a transfer.
If you don't see a 'Load Sample' button, you did not place a pellet in the beaker to weigh. Press 'Use Bench Scale' and weigh a benzoic acid pellet before using the oxygen bomb again.
If you don't see a 'Load Sample' button, you did not place a pellet in the beaker to weigh. Press 'Use Bench Scale' and weigh a benzoic acid pellet before using the oxygen bomb again.
The sample in the bomb is ignited by a thin wire that can be remotely heated. This fuse wire is suspended between two posts and presses against the pellet. Press the 'Add Fuse Wire' button to attach the fuse.
During combustion, this wire produces some 10's of joules of extra heat. For a rigorous result, the heat produced by the burnt portion of fuse wire should be subtracted from the calculated heat of combustion for the sample.
During combustion, this wire produces some 10's of joules of extra heat. For a rigorous result, the heat produced by the burnt portion of fuse wire should be subtracted from the calculated heat of combustion for the sample.
Now the bomb is ready to be closed. During the combustion reaction, the pressure and temperature inside the bomb will rise dramatically. Hence the name bomb. The bomb head mates with a heavy can and the entire assembly is secured by a thick threaded ring.
When assembling the bomb, be careful not to disrupt the sample or break the delicate fuse wire.
Press 'Close O2 Bomb' to assemble the bomb.
When assembling the bomb, be careful not to disrupt the sample or break the delicate fuse wire.
Press 'Close O2 Bomb' to assemble the bomb.
In order to ensure complete combustion, the reaction occurs in the presence of an extreme excess of oxygen. A high pressure oxygen tank is used to pressurize the bomb to about 30 atmospheres, or about 440 psi (pounds per square inch).
To pressurize the bomb, attach the hose from the oxygen tank by sliding the special fitting onto the filling stem. Press 'Attach O2 Hose' to do this.
To pressurize the bomb, attach the hose from the oxygen tank by sliding the special fitting onto the filling stem. Press 'Attach O2 Hose' to do this.
Now that the filling hose is attached we will use the compressed oxygen tank to pressurize the bomb.
Press 'Use O2 Tank'.
Press 'Use O2 Tank'.
The oxygen tank is a thick walled cylinder pressurized to several thousand psi. To use the gas a regulator is attached to the main valve. The regulator reduces the extreme pressure of the tank to more managable values.
When using an oxygen regulator it is important to not use any grease or oils as these can become flammible or explosive when exposed to high pressure oxygen.
When using an oxygen regulator it is important to not use any grease or oils as these can become flammible or explosive when exposed to high pressure oxygen.
Before opening the main,
high-pressure valve it is important to check that the
black reducing knob is set to zero pressure (spins loosely).
Open the main valve by
pressing 'Open Main Valve'.
The right-most pressure
gauge will show the pressure within the tank which should
be about 3000 psi.
high-pressure valve it is important to check that the
black reducing knob is set to zero pressure (spins loosely).
Open the main valve by
pressing 'Open Main Valve'.
The right-most pressure
gauge will show the pressure within the tank which should
be about 3000 psi.
Increase the oxygen pressure delivered to the bomb by pressing 'Increase Regulator Pressure'. Keep increasing the pressure until it reaches about 30 atm or 440 psi. Too low a pressure may lead to incomplete combustion within the bomb and an inaccurate value. Too high may lead to emergency venting of hot gases.
Once the target pressure has been reached, press 'Close Main Valve'.
Once the target pressure has been reached, press 'Close Main Valve'.
The bomb is now pressurized with oxygen. Return to the bomb to remove the filling hose.
Press 'Use O2 Bomb'.
Press 'Use O2 Bomb'.
The filling stem contains a one-way valve. Removing the filling hose will not allow any oxygen to escape. Slide the filling ring off the stem by pressing 'Remove O2 Hose'.
Any residual pressurized oxygen in the filling line escapes at this point. Since the main valve is closed, it is only a short burst.
Any residual pressurized oxygen in the filling line escapes at this point. Since the main valve is closed, it is only a short burst.
Before we can continue we need to reset the regulator valve. If the regulator valve is in the 'on' position when the main valve is opened next time, the pressure shock could damage the regulator. Also, resetting the regulator is a courtesy to the next user.
Press 'Use O2 Tank' to adjust the regulator.
Press 'Use O2 Tank' to adjust the regulator.
Turn the regulator knob
counter-clockwise until it feels loose. At this point it is set to zero pressure. Use the 'Decrease Regulator Pressure' to do this.
When the pressure adjustment has been set to zero the 'Use O2 Bomb' button appears. Press it.
counter-clockwise until it feels loose. At this point it is set to zero pressure. Use the 'Decrease Regulator Pressure' to do this.
When the pressure adjustment has been set to zero the 'Use O2 Bomb' button appears. Press it.
Since we plan to measure the heat released by the combustion of our sample we need to place the oxygen bomb into a thermally isolated container. We will call this well insulated container the thermos.
The thermos contains exactly 2 litres of water which, combined with the mass of the bomb itself, will provide the thermal mass to capture and hold the heat for us to measure.
Press the 'Insert Into Thermos' button to continue.
The thermos contains exactly 2 litres of water which, combined with the mass of the bomb itself, will provide the thermal mass to capture and hold the heat for us to measure.
Press the 'Insert Into Thermos' button to continue.
The thermos features electrical contacts which will connect with the oxygen bomb and allow remote firing of the fuse. It also contains a small stirrer to hasten thermal equilibrium. Finally, embedded temperature probes are connected to a display where we can monitor the temperature both before and after combustion.
The control unit displays the elapsed time since being turned on and the temperature inside the thermos. The upper 'LED' is lit when the fuse wire is intact and goes out once the fuse is burnt. The lit 'Fire' button ignites the fuse.
Record a temperature baseline every 30 seconds for a minute or so, then 'fire' the fuse. Record the temperature every 30 seconds until the temperature stabilizes after about 5 minutes. When you are done, press 'Remove From Thermos'.
Record a temperature baseline every 30 seconds for a minute or so, then 'fire' the fuse. Record the temperature every 30 seconds until the temperature stabilizes after about 5 minutes. When you are done, press 'Remove From Thermos'.
The inside of the bomb is still under extreme pressure which we need to release. The bomb has a venting valve that will allow the internal pressure to slowly drop to the ambient pressure.
Press 'Vent O2 Bomb' to release the unreacted oxygen and combustion products.
Press 'Vent O2 Bomb' to release the unreacted oxygen and combustion products.
It is now safe to open the bomb.
Press 'Open O2 Bomb' to disassemble the bomb.
Press 'Open O2 Bomb' to disassemble the bomb.
You can see that some portions of the fuse did not burn. Fuses come in standard lengths with a well known heat of combustion per centimeter. Before cleaning the bomb, you would normally measure the length of unburnt fuse and determine how many joules of heat were released by the burnt portion. For this experiment we will assume that our fuse produces a negligible amount of heat and will omit this step.
Press 'Clean O2 Bomb' to clean and dry the bomb for reuse.
Press 'Clean O2 Bomb' to clean and dry the bomb for reuse.
At this point you are ready to calculate the heat capacity of the calorimeter, Cv. You will recall that
∆H(combustion) = -Cv(T2 - T1) + RT(combustion)∆n(gas)
By rearrangement this gives
Cv = - (∆H(combustion) - RT(combustion)∆n(gas)) / (T2 - T1)
Cv = - ( [ -26.42 x weight benzoic acid(g) ] - [ 0.00831 x 298 x (7 - 15/2) ] ) / (T2 - T1)
Use your measured weight of benzoic acid and calorimeter temperatures to calculate Cv.
∆H(combustion) = -Cv(T2 - T1) + RT(combustion)∆n(gas)
By rearrangement this gives
Cv = - (∆H(combustion) - RT(combustion)∆n(gas)) / (T2 - T1)
Cv = - ( [ -26.42 x weight benzoic acid(g) ] - [ 0.00831 x 298 x (7 - 15/2) ] ) / (T2 - T1)
Use your measured weight of benzoic acid and calorimeter temperatures to calculate Cv.
Cv = -( -26.42 x weight benzoic acid(g) - 0.00831 x 298 x (7 - 15/2)) / (T2 - T1)
Recall that -26.42 is the heat of combustion of benzoic acid in kJ/g.
The value 0.00831 is the gas constant R in kJ/K·mol
The expression (7 - 15/2) is the number of moles of gaseous products minus the number of moles of gaseous reactants for the combustion of benzoic acid.
Recall that -26.42 is the heat of combustion of benzoic acid in kJ/g.
The value 0.00831 is the gas constant R in kJ/K·mol
The expression (7 - 15/2) is the number of moles of gaseous products minus the number of moles of gaseous reactants for the combustion of benzoic acid.
In this final portion of the experiment you will determine the ∆H(combustion) of an unknown compound similar to sucrose. This sample is identified by a 4 digit number.
8932
Be sure to record this number as you will need it when reporting your results.
The bomb calorimeter that you will be using has been calibrated for you and has a heat capacity of 9.294 kJ/K.
Unknown Compound + n O2(g) → n CO2(g) + m H2O(I)
Here, the n implies that the moles of O2 used and moles of CO2 produced are identical.
You will determine the ∆H(combustion) of the unknown sample by following the same steps that you used to determine the Cv of your calorimeter in part two of this experiment.
The heat of combustion you calculate will be for the total sample and in kJ. To report your value you should convert it to kJ/g by dividing by the sample weight.
The heat of combustion you calculate will be for the total sample and in kJ. To report your value you should convert it to kJ/g by dividing by the sample weight.
Here are the steps to follow
- Use the bench scale and weigh a pellet of the unknown sample.
- Load the bomb head with the pellet and fuse, and assemble the bomb.
- Pressurize the bomb, leaving the oxygen tank ready for reuse.
- Seal the bomb in the thermos and record the temperature changes after ignition.
- Remove and vent the bomb and then clean it for reuse.
Steps
- Weigh the unknown sample
- Load the sample & fuse
- Close the bomb
- Pressurize with ~440psi O2
- Seal the bomb in the thermos
- Record the base temperature
- Ignite the sample
- Record the temperature until the readings stabilize
- Remove & vent bomb
- Clean up the bomb
- Calculate ∆H(combustion)
Press the 'Done' icon when
you are completely finished.
- Weigh the unknown sample
- Load the sample & fuse
- Close the bomb
- Pressurize with ~440psi O2
- Seal the bomb in the thermos
- Record the base temperature
- Ignite the sample
- Record the temperature until the readings stabilize
- Remove & vent bomb
- Clean up the bomb
- Calculate ∆H(combustion)
Press the 'Done' icon when
you are completely finished.
All Done !
Continue Working

 Next
Next Skip
Skip
Loading Assets..0%